| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 오류역전파
- 인공지능 수학
- 인공지능
- 딥러닝
- HMM
- bioinformatics
- 생물정보학
- 캐글
- 바이오파이썬
- 시그모이드
- AP Computer Science A
- RNN
- AP
- 파이썬
- 인공신경망
- COVID
- 생명정보학
- 바이오인포매틱스
- CNN
- Java
- Kaggle
- BLaST
- 블록체인
- 자바
- 서열정렬
- MERS
- ncbi
- 이항분포
- SVM
- 결정트리
- Today
- Total
데이터 과학
인공지능 행렬 본문
인공지능 수학에서 가장 기본이 되는 이론입니다.
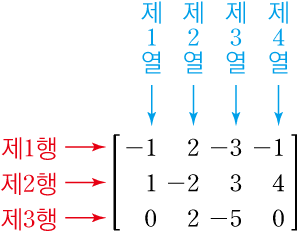
행(가로줄)과 열(세로줄)로 이루어졌기 때문에 행렬로 이름을 붙였습니다.
인공신경망 프로그래밍 할 때 입력값과 가중치 값을 연산해야 하는데 이때 도움이 되는 수학이론이 행렬입니다.
오류역전파 이론에서는 처음부터 행렬이론을 사용했던 것은 아니었고, 자주 사용하다보니 그리고 numpy에서 쉽게 제공이 되기에 파이썬으로 프로그래밍 할 때 numpy 안에 행렬 함수를 적용해서 사용하면 편하기 때문에 고착화 되었습니다.
행렬이전에는 연립방정식의 해를 찾는 방법으로 수식을 프로그래밍해서 만들었는데 힘든 작업이었죠.
연립방정식 예제 -
연립방정식의 해가 많아지면서 이를 프로그램으로 옮기고 계수(coefficent)값을 찾아 내는 것이 여간 힘든일이 아니었습니다. 그래서 인공 신경망 연산을 할 때 좀 더 쉽게 만들어낸 부분이 행렬입니다.
미지수인 계수를 나타내는 행렬에 대한 연산을 하는 것을 계수행렬이라고 하는데 이는 아래 사이트 내용을 참고하면 됩니다.
http://matrix.skku.ac.kr/sglee/linear/ocu/20102.html
1.2 행렬
'98 선형대수학 OCU 1장 2절 웹노트(LA Web Note) 이곳은 열린가상대학(Open Cyber University)에 소개하는 이상구 교수(Dr. Sang-Gu Lee) 의 Linear Algebra WebNote 입니다. 학부 선형대수학의 강의록과 과제, Quiz와
matrix.skku.ac.kr
아나콘다 쥬피터 노트북에서 다음과 같이 실행하면 간단한 결과가 나옵니다.
x는 입력값이고, w는 가중치(웨이트)값입니다.
import numpy as np
x = np.array([1,2])
w = np.array([[3,4,5],[6,7,8]])
print(x)
print(w)
y = np.dot(x,w)
print(y)
[1 2]
[[3 4 5]
[6 7 8]]
[15 18 21]
dot이라는 명령어는 내적의 명령어로 행령의 곱을 나타냅니다.
np.array( [1, 2, 3] )
행렬값을 나타내는 명령어와 shape을 통해 배열의 형상을 반환하는 명령어도 있습니다.
y.shape
x.shape
차원(dimension)을 나타내는 명령어도 있으면서 이를 적용해서 전체 행렬의 구조를 나타낼 수 있습니다.
np.ndim(y)
행렬의 합
행의 개수와 열의 개수가 같은 행렬은 연산을 할수 있습니다. 같은 위치에 있는 값을 더하거나 뺄수 있는데 예제를 통해 한번 내용을 보도록 하죠.
다음은 2*3 행렬입니다.
A=[123] [456] , B=[234] [567] 로 정의를 내린 다음 두 행렬을 더하면 [356] [9 11 13] 이라는 결과가 나옵니다.
이를 파이썬으로 프로그래밍 하면 다음과 같은 예제를 만들어 낼 수 있습니다.
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[2,3,4],[5,6,7]])
print(A+B)
[[ 3 5 7]
[ 9 11 13]]행렬은 간단하게 배수의 연산도 가능한데 다음과 같은 결과를 얻을 수 있습니다.
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
print(3*A)
[[ 3 6 9]
[12 15 18]]
행렬의 곱
벡터에서의 벡터끼리 내적(dot)을 행렬에 적용하면 행렬의 곱이 됩니다.
예제를 통해 행렬의 연산에 대해 이해해 보면 다음과 같습니다.
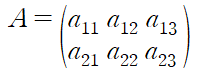
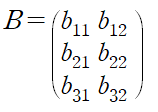

위에 보면 계수행렬이라는 용어가 있다고 했는데 인공신경망에서는 b에 해당하는 미지수 값을 계수라고 만들어 놓으면 되고, a는 입력값으로 연산을 만들어서 방정식을 구성하면 됩니다.
행과 열로 값을 연산하는 방법이 행렬 곱입니다.
파이썬으로 예제를 하나 보면 2*3 행렬과 2*3 행렬의 연산에서는 에러가 나타납니다.
첫번째 3개의 열과 두번째 2개의 행은 갯수가 맞지 않아서 연산이 안된다는 문제가 있습니다.
에러를 없앨려면 첫번째 3개의 열과 두번째 3개의 행으로 값을 맞춰줘야 합니다.
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[2,3,4],[5,6,7]])
print(np.dot(A,B))
ValueError: shapes (2,3) and (2,3) not aligned: 3 (dim 1) != 2 (dim 0)
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[2,3,4],[5,6,7], [8,9,10]])
print(np.dot(A,B))
[[ 36 42 48]
[ 81 96 111]]
아다마르 곱 - 행렬의 요소마다 곱하는 방법입니다. 단순한 배열 연산입니다.
A=[0 1 2] [3 4 5] [6 7 8] , B=[1 2 3] [4 5 6] [7 8 9]
import numpy as np
A = np.array([[0,1,2],[3,4,5],[6,7,8]])
B = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(A*B)
[[ 0 2 6]
[12 20 30]
[42 56 72]]
전치 행렬
전치라는 의미는 행과 열을 바꿔주는 의미입니다.
A=[1 2 3] [4 5 6]
A (T) = [1 4] [2 5] [3 6]
import numpy as np
A = np.array([[0,1,2],[3,4,5],[6,7,8]])
print(A.T)
[[0 3 6]
[1 4 7]
[2 5 8]]인공신경망에서 전치행렬을 쓰는 이유는 오차값을 통해 역전파로 값을 부텨 할 때 가중치 값을 올바르게 반영하기 위해서 전치 행렬을 써야 합니다.
이 내용은 아래 블로그에 잘 나와 있습니다.
오류역전파의 간단한 원리
인공 신경망에서의 오류역전파는 입력과 은닉층(Hidden layer)의 연산의 결과와 활성화 함수(activate function)의 발산으로 구성되어 있다. 1. 입력값과 은닉층의 연산의 결과 2. 연산의 결과에 대한 활
tsyoon.tistory.com
역행렬
행렬식에서 단위행렬을 통해 역행렬을 구할 수 있습니다.
단위행렬은 행과 열의 수가 같고 대각선이 1이고 이외에는 0으로 채워진 행렬입니다.
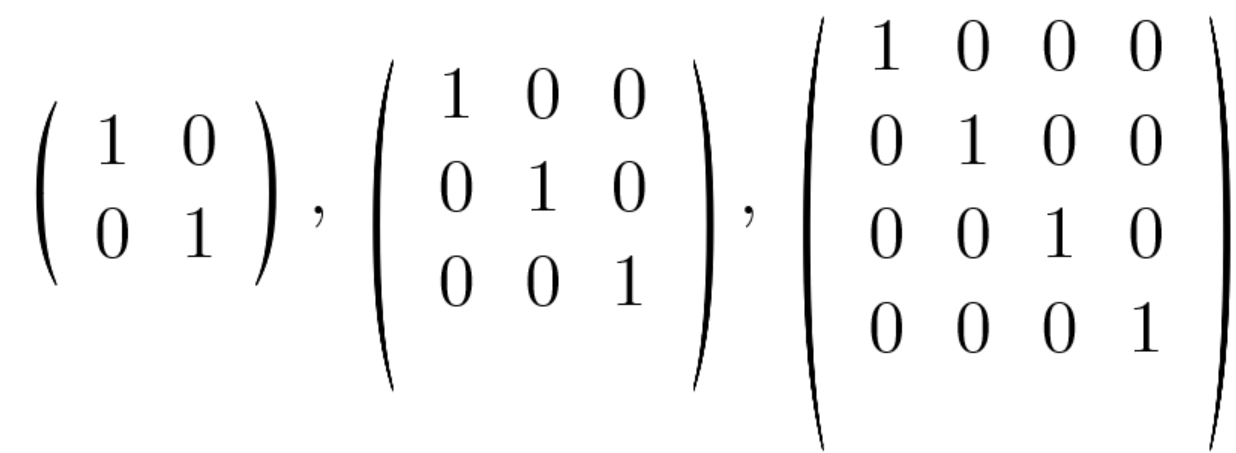
import numpy as np
print(np.eye(3))
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]A*A(-1)=E, 여기서 E는 단위행렬입니다.
A = [1 2] [3 4] 에 대한 역행렬을 구해보겠습니다.
import numpy as np
A=np.array([[1,2],[3,4]])
print(np.linalg.inv(A))
[[-2. 1. ]
[ 1.5 -0.5]]
https://ratsgo.github.io/linear%20algebra/2017/03/14/operations/
기초 행렬연산 · ratsgo's blog
이번 포스팅에서는 머신러닝, 데이터마이닝 기초인 행렬 연산(Matrix Operations)에 대해 다뤄 보려고 합니다. 연산의 정의 정도를 간단히 다루는 것이니 깊은 내용을 원하시는 분들은 이곳을 참고
ratsgo.github.io
https://datalabbit.tistory.com/27
[행렬대수학] 행렬대수학(Matrix Algebra) 기초 - 행렬(Matrix)
안녕하십니까, 간토끼입니다. 이번 카테고리에서는 Matrix Algebra, 행렬대수학에 대해 다뤄보도록 하겠습니다. 보통은 선형대수학(Linear Algebra)를 다루는 게 일반적인데요. 굳이 행렬대수학이라고
datalabbit.tistory.com
'인공지능 > 인공지능과 수학' 카테고리의 다른 글
| 인공지능, 접선의 기울기와 경사하강법 (0) | 2022.08.01 |
|---|---|
| 인공지능 편미분 (Partial Derivative) (0) | 2022.08.01 |
| 인공지능 벡터, 텐서 (0) | 2022.07.31 |
| 인공지능 기초함수 (0) | 2022.07.31 |
| 인공지능과 수학 (0) | 2021.07.20 |



