| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 인공지능 수학
- COVID
- bioinformatics
- 인공지능
- Java
- CNN
- RNN
- 파이썬
- 딥러닝
- HMM
- 자바
- MERS
- AP Computer Science A
- 바이오인포매틱스
- 결정트리
- 서열정렬
- BLaST
- SVM
- 생명정보학
- 오류역전파
- 시그모이드
- 이항분포
- 인공신경망
- 블록체인
- 생물정보학
- ncbi
- 캐글
- 바이오파이썬
- AP
- Kaggle
- Today
- Total
데이터 과학
인공지능, 접선의 기울기와 경사하강법 본문
인공신경망을 공부하다보면 필연적으로 마주쳐야 하는 이론이 경사하강법(gradient desendent) 이론입니다.
가중치 값에 대한 변화율을 만들기 위해 변화된 값을 찾는 방법으로 오류역전파 알고리즘에 적용되어 오늘날 널리 사용되고 있습니다. 수학적 지식으로 미적분학(calculus)에서 전미분과 편미분에 대한 이해가 필요합니다.
고등학교 수학과정에 극한과 미분에 대한 내용이 있으므로 오류역전파의 경사하강법을 이해하는 부분에 있어서는 어렵지 않을 것입니다.
이를 설명을 하려면 속력의 의미로 사용되는 내용으로 순간속도에 대한 내용으로 정의를 하려고 하는데 이때 극한의 개념이 사용됩니다.
운전을 할때 시속60km에서 차의 속도가 70km, 80km로 변화가 된다는 부분을 이해하면 보다 쉽게 생각할 수 있습니다. 이런 변화에 대한 내용을 수치적으로 표현하는 것이 미분인데, 이 변화에 대한 내용을 인공신경망에서 적용하여 경사하강법 이론을 반영하는 것입니다.
이렇게 하면 가중치(weight)값에 대한 변화값을 찾아내어 목적값의 오차를 줄일 수 있어 학습(trainning)을 진행할 수 있는 것입니다.
오류역전파에 대한 원리는 아래 내용에서 설명이 되어 있습니다.
오류역전파의 간단한 원리
인공 신경망에서의 오류역전파는 입력과 은닉층(Hidden layer)의 연산의 결과와 활성화 함수(activate function)의 발산으로 구성되어 있다. 1. 입력값과 은닉층의 연산의 결과 2. 연산의 결과에 대한 활
tsyoon.tistory.com
신경망 관련 미분 관련 내용은 많은 책에서 소개를 하고 있고, 고등학교 수학과정에도 나와 있으니 이론적인 내용에 대해 설명을 하고 코딩은 시그모이드 함수에 대한 미분을 하는 것으로 프로그래밍을 하면 오류역전파가 프로그램이 완성이 되겠습니다.
평균변화율은 직선의 기울기


미분계수는 순간변화율로 접선의 기울기의 의미로 계산하면 됩니다.
델타 x가 0으로 수렴한다는 극한으로 정의를 내리면 미분계수값이 나오는데 y=f(x)는 x=a에서 미분가능하다고 정의합니다. 미분이 순간 변화율이기 때문에 접선의 기울기로 설명할 수 있습니다.
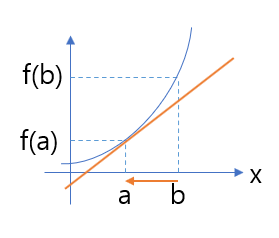
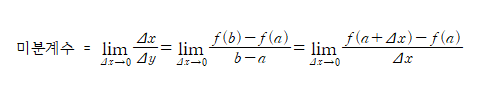
도함수의 개념은 함수 y=f(x)의 정의역에 미분계수 f프라임()를 대응한다라는 의미입니다. 이때 델타 x를 h로 변환하여 표현하면 다음과 같습니다.

이처럼 미지수 x를 표현함으로 인해 다른 변수들의 다양성을 일반화 했다고 할 수 있습니다.
이렇게 평균변화율, 미분계수, 도함수의 개념이 순차적으로 정리가 됩니다.
인공신경망에서는 이 내용을 가지고 변화율이라는 내용으로 적용해서 오류역전파에서 역전파의 가중치 값을 조정하는데 반영합니다.
판별함수인 Sigmoid 함수도 미분을 해서 변화율을 반영하는데 그 공식은 다음과 같습니다.
몫의 미분법 -

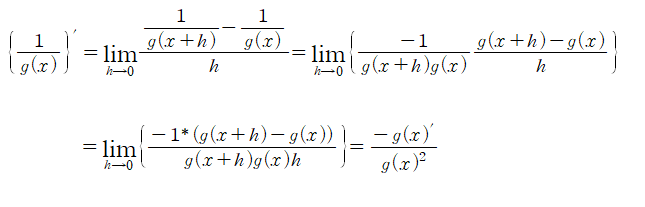
시그모이드 함수를 미분하기 위해서는 몫의 미분법을 알아야 합니다.

또는 연쇄법칙을 이용한 음함수 미분법으로 간단히 미분을 하면 다음과 같습니다.
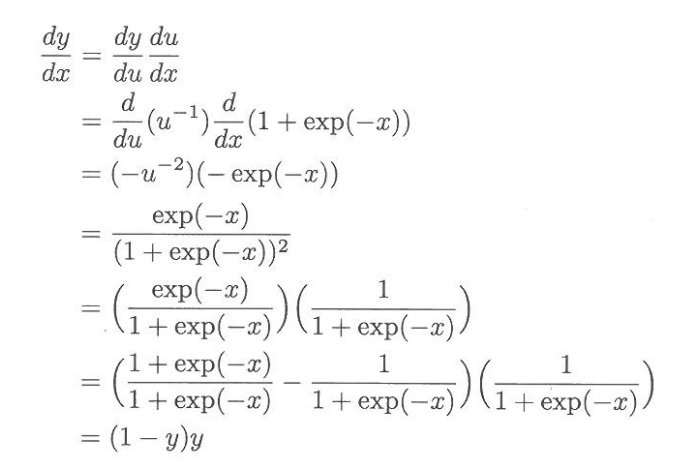
시그모이드 미분에서는 지수미분에 대한 이해도 있어야 합니다. 지수미분에 대한 규칙은 간단합니다.
https://color-change.tistory.com/50
지수함수의 미분, 자연로그의 미분 증명
::지수함수의 미분, 자연로그의 미분 증명:: - (e^x-1)/x, e^x, a^x, ln(x), loga(x) 이 포스팅은 지수함수의 미분(e^x-1/x, e^x), 자연로그(lnx)의 미분에 관한 글 입니다. 자연상수는 파이(pi)와 함께 거론되..
color-change.tistory.com
그리고, 지금까지의 내용은 전미분에 대한 간단한 내용이었으며 오류역전파에서는 다변수가 있어서 편미분을 합니다.
그 내용은 편미분편을 참고해 주세요.
편미분 (Partial Derivative)
고등학교 교육과정에는 없으며 대학교 공업수학에서 나오는 내용인데 요즘은 인공신경망에서 나오는 내용으로 전미분 이후에 학습하고 있습니다. 편미분의 의미는 간단합니다. 여러변수들이
tsyoon.tistory.com
'인공지능 > 인공지능과 수학' 카테고리의 다른 글
| 인공지능, 순열과 조합 (이항분포) (0) | 2022.08.02 |
|---|---|
| 인공지능 확률 (0) | 2022.08.02 |
| 인공지능 편미분 (Partial Derivative) (0) | 2022.08.01 |
| 인공지능 벡터, 텐서 (0) | 2022.07.31 |
| 인공지능 행렬 (0) | 2022.07.31 |



