| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- AP Computer Science A
- 서열정렬
- 캐글
- Kaggle
- 인공지능
- bioinformatics
- AP
- 시그모이드
- 자바
- 인공신경망
- ncbi
- 블록체인
- HMM
- 오류역전파
- MERS
- 생명정보학
- BLaST
- 딥러닝
- CNN
- RNN
- 결정트리
- 생물정보학
- 바이오파이썬
- 인공지능 수학
- 바이오인포매틱스
- COVID
- SVM
- 파이썬
- Java
- 이항분포
- Today
- Total
데이터 과학
이항분포에서 정규화 본문
이항분포는 discrete 분포에서 이항확률(Binomial)을 계산하는 방법입니다.
N값이 커질 경우 이항확률로 계산하는 방법보다 정규분포 방법으로 계산하는 방법이 훨씬 더 쉬울 수 있습니다.
단지, 이항분포는 계산되는 이항식으로 계산하기에 수치적으로 분석할 수 있으나, 정규분포의 경우는 확률분포로 표현해서 면적을 가지고 확률값을 계산하기 때문에 연속 확률 구간에 대해 명시적으로 접근해야 합니다.
이항분포는 수치적인 접근으로 정규분포는 구간에 따른 면적으로 계산하는 방법으로 차이가 있습니다.
하나의 예제를 통해 이를 설명해 보겠습니다.
예제1)
어떤 공장에서 나오는 자동차 중 15%가 결함이 있다고 합니다.
자동차 50대가 생산될 때, 6대의 자동차에 결함이 있을 확률은 얼마인지를 알아봅시다.

(50! / (44!*6!)) (.15)^6 (.85)^44 = 0.1419
TI 계산기를 사용하면 간단히 계산됩니다.
여기서 평균값을 계산하면 np = 50*0.15=7.5
표준편차는 루트(npq) = 루트(50*0.15*0.85)= 2.525
이를 정규분포로 나타내면 아래 그림과 같습니다.

https://homepage.stat.uiowa.edu/~mbognar/applets/normal.html
정규분포 그려주는 사이트에서 분포를 한번 나타내 봤습니다.
이렇게 하면 전체 확률분포가 0.27624라는 결과가 나옵니다.
그런데 이항분포를 정규분포식으로 이렇게 계산해서 결과값을 나타내면 안 됩니다. 그 이유가 정규분포는 선에 대한 확률은 없습니다. 면적이 확률이기 때문에 면적을 나타내야 합니다.
그렇다면 x=6이 포함되는 면적을 나타내야겠죠. 분포가 6.5와 5.5 인 값을 설정해서 이 값의 차이값을 나타내야 합니다.
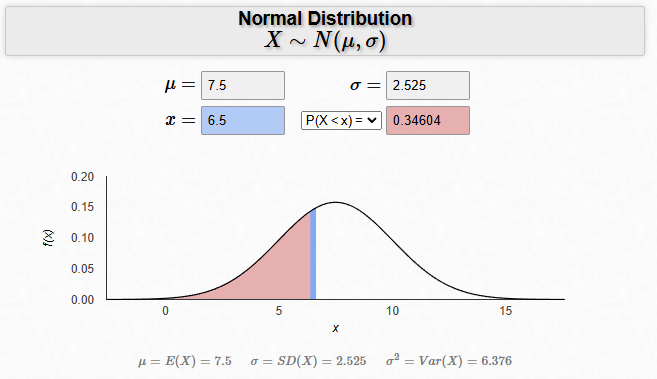

0.34604-0.21416 = 0.13188
이런 방법으로 결과값을 가져올 수 있습니다. 이항분포식에서 나온 결과인 0.1419 값과는 오차가 있지만 계산방법이 쉽고 N개가 많을수록 이 오차범위가 상당히 줄어들게 됩니다.
N개의 값이 많아지는 빅데이터에 있어서는 이항확률로 접근하는 것 보다는 정규분포로 계산해서 면적에 대한 분포를 찾는 방법이 더 효율적입니다.
'AP > AP Statistics' 카테고리의 다른 글
| 모수와 통계량 (0) | 2025.01.13 |
|---|---|
| 모수와 비모수 (0) | 2025.01.12 |
| 정성적 데이터와 정량적 데이터 (0) | 2025.01.12 |
| 기술 통계학과 추론 통계학 (0) | 2025.01.12 |
| 신뢰구간 문제 풀이 (0) | 2023.04.25 |
