| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- RNN
- HMM
- 바이오파이썬
- 인공지능
- MERS
- 서열정렬
- ncbi
- 캐글
- CNN
- 시그모이드
- Kaggle
- BLaST
- 생물정보학
- 파이썬
- 인공신경망
- 딥러닝
- SVM
- bioinformatics
- 자바
- AP
- COVID
- 바이오인포매틱스
- Java
- 블록체인
- 이항분포
- 결정트리
- AP Computer Science A
- 인공지능 수학
- 생명정보학
- 오류역전파
- Today
- Total
데이터 과학
자유도 본문
통계학에서 자유도(degree of freedom)란, 통계적 추정이나 가설 검정 등의 분석에서 모집단의 특성을 설명하기 위한 파라미터의 수를 나타내는 개념입니다.
자유도는 표본의 크기와 모집단의 크기에 따라 결정됩니다. 일반적으로 표본의 크기가 커질수록 자유도는 증가하고, 모집단의 크기가 커질수록 자유도는 감소합니다.
예를 들어, 표본의 분산을 계산할 때, 이전 표본들의 평균값을 사용하여 계산합니다. 이때, 평균값은 이미 결정되어 있으므로, 다음 표본의 값을 자유롭게 선택할 수 없습니다. 따라서 자유도는 n-1로 설정됩니다. 여기서 n은 표본의 크기입니다. 이렇게 자유도가 n-1이 되면, 표본 분산이 모집단 분산의 추정값이 됩니다.
자유도는 다른 통계 분석에서도 중요한 역할을 합니다. 예를 들어, t-검정에서는 자유도가 t-분포의 모양을 결정하고, 카이 제곱 검정에서는 자유도가 카이 제곱 분포의 모양을 결정합니다.
따라서 자유도는 통계학에서 매우 중요한 개념 중 하나이며, 통계적 추정 및 가설 검정 분석에서 파라미터의 수를 결정하는 데 사용됩니다.
예를 들어, 5명의 학생들의 수학 시험 점수가 다음과 같다고 가정해 봅시다: 70, 75, 80, 85, 90. 이때, 이 학생들의 평균 점수와 분산을 구해보려고 합니다.
우선 평균 점수를 계산하면 다음과 같습니다:
(70 + 75 + 80 + 85 + 90) / 5 = 80
이제 분산을 계산하기 위해, 각 학생의 점수에서 평균 점수를 뺀 뒤 제곱합니다. 그리고 그 결과를 모두 더한 다음, 학생 수(n)에서 1을 뺀 자유도(degree of freedom)로 나눠줍니다. 수식으로 나타내면 다음과 같습니다:
s^2 = Σ(xi - x̄)^2 / (n - 1)
여기서 xi는 각 학생의 점수를 나타내며, x̄은 전체 학생들의 평균 점수입니다. 그리고 n은 학생 수입니다.
따라서 위의 예제에서, 분산을 계산하는 식은 다음과 같습니다:
s^2 = [(70-80)^2 + (75-80)^2 + (80-80)^2 + (85-80)^2 + (90-80)^2] / 4
이를 계산하면:
s^2 = 125
즉, 이 학생들의 수학 시험 점수의 분산은 125입니다. 이때, 자유도는 n-1로 설정됩니다. 즉, 이 예제에서는 자유도가 4입니다. 이것은 이전 학생들의 점수를 이미 알고 있기 때문에, 다음 학생의 점수를 자유롭게 선택할 수 없기 때문입니다. 따라서, 이 분산은 이 학생들의 수학 시험 점수의 모집단 분산의 추정값이 됩니다.
모집단 분산(population variance)은 모집단의 모든 개체에 대한 분산을 의미합니다. 모집단을 전부 조사하는 것은 현실적으로 어렵기 때문에, 우리는 일부 샘플 데이터를 사용하여 모집단 분산을 추정할 수 있습니다. 이때, 추정한 모집단 분산의 값은 모집단의 실제 분산 값과 다를 수 있습니다.
따라서, 우리는 표본 분산(sample variance)을 사용하여 모집단 분산의 추정값을 계산합니다. 표본 분산은 각 데이터 값이 표본 평균으로부터 얼마나 떨어져 있는지를 나타내는 값으로, 다음과 같은 식으로 계산됩니다:
s^2 = Σ(xi - x̄)^2 / (n - 1)
여기서 xi는 각 데이터 값, x̄은 표본의 평균, n은 표본의 크기입니다.
따라서, 표본 분산을 사용하여 모집단 분산을 추정할 때, 표본 분산이 모집단 분산과 일치하지 않을 수 있기 때문에, 이러한 추정값은 오차를 가지고 있을 수 있습니다. 이 오차는 표본의 크기가 작을수록 커지는 경향이 있습니다. 따라서, 통계적 추론에서는 이러한 오차를 고려하여 적절한 통계적 방법을 선택해야 합니다.
증명 방법은 아래와 같습니다. 표본평균 기댓값은 모평균과 같으며, 표본분산의 기댓값은 모분산과 같습니다.
표본평균 기댓값

표본분산

표본분산 기댓값
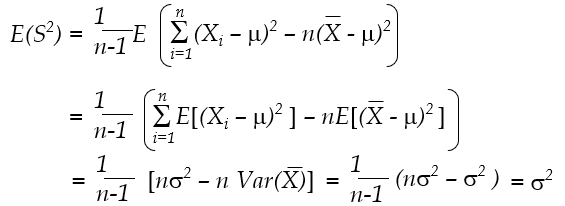
'AP > AP Statistics' 카테고리의 다른 글
| 신뢰구간 문제 풀이 (0) | 2023.04.25 |
|---|---|
| 이항분포 (0) | 2023.04.16 |
| 실험과 관찰학습 (0) | 2023.01.09 |
| AP Statistics 시작 (0) | 2023.01.01 |
| 편향 Bias (0) | 2022.09.06 |


