인공신경망에서 시그모이드 함수

인공신경망에 대해서 공부하려면 함수(function)의 의미에 대해 이해를 해야 합니다. 

 

퍼셉트론을 사용할 때 함수의 개념을 이용하여 경계를 기준으로 값을 변환시키는 형태로 알고리즘을 작성하기 때문입니다. 어떤 경계를 만들어서 판별해야 합니다. 

 

그 경계가 선형방정식이고, 그 결과 값을 다른 형태로 바꿔주는 기능이 필요한 것입니다. 

 

초기에는 Step Function을 사용하다 이후에는 Sigmoid Function을 사용합니다. (현재는 주로 ReLU Function을 사용합니다.) 

 

 

Step Funtion: 

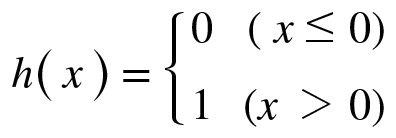
import numpy as np
import matplotlib.pylab as plt
# 계단 함수 구현
def step_function(x):
    return np.array(x>0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x,y)
# y축 범위 지정
plt.ylim(-0.1,1.1);
plt.show()

 

 

 

 

Sigmoid Function :

 

 

 

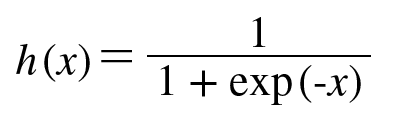
import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1/(1+np.exp(-x))
x = np.array([-1.0,1.0,2.0])
print(sigmoid(x))

x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1); 
plt.show()

 

 

시그모이드 함수는 인공신경망에서 가장 기본적인 활성화 함수 중 하나입니다. 입력값을 0과 1 사이의 값으로 변환시켜주는 함수로, 이를 통해 출력값을 확률로 해석할 수 있습니다.

인공신경망에서는 입력값을 여러 개의 노드로 구성된 입력층에서 받아들이고, 각 노드에는 가중치와 편향이 적용되어 값을 계산합니다. 이 계산 결과를 활성화 함수를 통해 변환하여 다음 계층으로 전달하게 됩니다.

이러한 변환 과정에서 가장 많이 사용되는 활성화 함수 중 하나입니다. 그 이유는 시그모이드 함수가 출력값을 0과 1 사이로 제한시켜주기 때문입니다. 이러한 제한을 통해 출력값을 확률로 해석할 수 있게 되며, 이를 이용하여 분류 문제에서 클래스에 속할 확률을 계산할 수 있습니다.

또한 시그모이드 함수는 미분 가능한 함수이기 때문에 역전파(backpropagation) 알고리즘을 이용하여 오차를 역전파시키는 데에도 용이합니다. 여기서 미분 가능하다라는 의미는 변화율을 적용하여 오차를 줄여 나간다라는 의미로 학습의 개념을 확장 시킬 수 있는 내용입니다. 

 

 

x1과 x2의 입력값을 1과 2로 정하고 가중치(weight)값을 0.1과 0.2, 0.3 etc으로 정해 준다면 출력값은 각각  [ 3.2  3.8  4.4] 으로 정해집니다. 

 

 

 

여기에 시그모이드 함수 값을 적용해서 발산시키면 다음과 같은 결과가 나타납니다. 

 

import math

def sigmoid(x):
  return 1 / (1 + math.exp(-x))

 

sigmoid(3.2)

0.9608342772032357

 

sigmoid(3.8)

 

0.9781187290638694

 

sigmoid(4.4)

 

0.9878715650157257

 

 

 

히든 노드에서의 값은 3.2 3.8 4.4 인데 비해 시그모이드 함수에 값을 넣으니 0.960 0.978 0.988 으로 값이 변환 됩니다. 

 

시그모이드 함수를 적용하는 이유는 실수값에 대해서는 스텝 함수보다는 보관력이 좋다고 평가 할 수 있기 때문입니다.

스텝함수는 데이터에 대한 보관력이 상실되어서 극과 극으로 판단하는 경우가 많아서죠. 

반면, 시그모이드는 0과 1사이에 있는 실수값을 변환하여서 값 자체의 보관련도 좋아지고 경사하강법에서 나타나는 기울기 폭주에 대한 문제도 해결 할 수 있는 장점이 있습니다. 

 

그맇지만 위의 예제에서도 알 수 있듯이 입력값에 대비하여 시그모이드 이후에 출력값에서 변환된 결과가의 범위가 그리 크지 않습니다.

 

3.2 3.4 4.4에서의 편차가 어느 정도 있는데 비해 시그모이드 함수를 통해 0.960 0.978 0.988 값이 나오는데 입력값에 비해 편차가 크지 않습니다. 이 문제가 차후에 나타나는 오류역전파에서의 히든 레이어 문제와 기울기 소실 문제점과 연결됩니다. 

 

출력값에 대한 편차를 크게 하는 방법에 대한 연구가 꾸준히 진행이 되어서 다른 함수를 사용해야 한다는 결론에 도달 했죠. 이에 대한 연구를 통해 딥러닝의 기반을 만들었다고 할 수 있습니다. 

 

 

https://tsyoon.tistory.com/144

인공신경망에서 행렬

 

https://gooopy.tistory.com/52

딥러닝-3.1. 활성화함수(2)-시그모이드 함수(Sigmoid)

 

 

오류역전파에서 시그모이드 함수를 사용하는 목적은 스텝함수의 한계점 문제로 사용한 알고리즘인데 초기에는 그럭저럭 간단한 문제점을 해결하는데 잘 사용이 되었는데 여러가지 문제점이 나타나게 됩니다. 

이러한 문제점을 해결하면서 딥러닝의 이론이 기반을 다지게 되었습니다.

 

그래도 시그모이드 함수의 역할과 사용방법에 대해 이해를 하면서 순전파와 역전파의 내용을 한번 찾아보면서 공부해 보는것이 오류역전파의 알고리즘 학습에 도움이 될 것이라 봅니다. 

 

https://www.google.com/search?q=%EC%98%A4%EB%A5%98%EC%97%AD%EC%A0%84%ED%8C%8C+%EC%82%AC%EC%9A%A9+%EC%9D%B4%EC%9C%A0&oq=%EC%98%A4%EB%A5%98%EC%97%AD%EC%A0%84%ED%8C%8C+%EC%82%AC%EC%9A%A9&aqs=chrome.1.69i57j33i160l2.5621j0j15&sourceid=chrome&ie=UTF-8&safe=active&ssui=on 

🔎 오류역전파 사용 이유: Google 검색