| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- HMM
- 생명정보학
- 딥러닝
- 자바
- 결정트리
- 서열정렬
- AP
- 인공지능 수학
- CNN
- 인공지능
- BLaST
- Kaggle
- 이항분포
- SVM
- COVID
- MERS
- 파이썬
- 오류역전파
- 바이오파이썬
- ncbi
- 캐글
- bioinformatics
- 시그모이드
- 인공신경망
- RNN
- 생물정보학
- 바이오인포매틱스
- 블록체인
- AP Computer Science A
- Java
- Today
- Total
데이터 과학
마르코프 모델과 벨만 방정식 본문
마르코프 모델은 시간에 따라 상태가 변하는 확률적 과정을 설명하는 모델로, 다음 상태가 오직 현재 상태에만 의존하는 성질을 가지고 있습니다. 이러한 성질을 마르코프 성(Markov Property)이라고 하며, “미래는 현재에 의해서만 결정된다”는 의미를 담고 있습니다. 즉, 과거의 정보가 아니라 현재의 상태만으로도 미래의 변화를 예측할 수 있다는 점이 핵심입니다.
현실 세계의 다양한 현상들은 이 마르코프 모델로 설명할 수 있습니다. 예를 들어 날씨의 변화, 로봇의 위치 이동, 재고의 변동, 사용자의 클릭 패턴 등은 모두 시간이 흐름에 따라 상태가 확률적으로 변화하는 과정입니다. 이러한 문제를 단순화하여 다루기 위해 마르코프 모델이 사용됩니다.
마르코프 모델에서는 가능한 모든 상태를 상태 집합 S로 나타내며, 현재 상태에서 다음 상태로 이동할 확률을 전이 확률 P(s’|s)로 표현합니다. 이 확률들을 표 형태로 정리한 것이 전이 확률 행렬(Transition Matrix)입니다.
마르코프 모델은 응용 형태에 따라 세 가지로 구분됩니다.
첫째, 단순히 상태만 시간에 따라 변하는 마르코프 체인(Markov Chain)이 있습니다.
둘째, 상태가 직접적으로 관찰되지 않고 간접적인 관측값을 통해 추정해야 하는 은닉 마르코프 모델(HMM, Hidden Markov Model)이 있습니다.
마지막으로, 상태뿐 아니라 행동(Action)과 보상(Reward)의 개념이 포함된 마르코프 의사결정 과정(MDP, Markov Decision Process)이 있습니다. 이 중 MDP는 인공지능의 강화학습(Reinforcement Learning)의 핵심적인 수학적 기반이 됩니다.
마르코프 의사결정 과정(MDP)의 구성요소
MDP는 다섯 가지 요소로 이루어집니다.
첫째는 상태(State, S), 둘째는 행동(Action, A), 셋째는 전이 확률(Transition Probability, P(s’|s,a)), 넷째는 보상 함수(Reward Function, R(s,a)), 마지막으로 할인율(Discount Factor, γ)입니다.
에이전트(agent)는 매 시점마다 정책(policy) π(a|s)에 따라 행동을 선택합니다. 그 결과로 새로운 상태로 전이되고, 즉시적인 보상을 얻게 됩니다. 이러한 과정을 반복하면서 에이전트는 장기적인 보상의 합, 즉 누적 기대 보상(Expected Return)을 최대화하는 정책을 찾아가게 됩니다.
가치(Value)의 개념
어떤 상태에서 앞으로 받을 수 있는 총보상의 기댓값을 가치(Value)라고 합니다. 정책 π를 따를 때의 상태 s의 기대 보상은 상태 가치 함수(Value Function, Vπ(s))로 표현하고, 특정 행동을 취했을 때의 기대 보상은 행동 가치 함수(Action-Value Function, Qπ(s,a))로 표현합니다.
또한, 할인율 γ(감마)는 미래에 받을 보상의 현재 가치를 결정하는 데 사용됩니다. γ가 0에 가까우면 즉시 보상을 중요하게 여기고, γ가 1에 가까우면 미래 보상까지 고려하게 됩니다. 일반적으로 강화학습에서는 γ 값을 0.9~0.99 사이로 설정합니다.
벨만 방정식(Bellman Equation)
벨만 방정식은 현재의 가치를 즉시 보상과 다음 상태의 기대 가치로 나누어 계산하는 수학적 원리입니다. 다시 말해, 어떤 상태의 가치는 “지금 당장의 보상”과 “다음 단계에서 얻을 수 있는 가치의 기대값”의 합으로 표현됩니다.
정책이 주어졌을 때의 벨만 방정식은 다음과 같습니다.

이 식은 정책 π를 따를 때 상태 s의 기대 보상이 현재 보상과 다음 상태의 가치의 기대값으로 구성되어 있음을 보여줍니다.
최적의 정책을 구하기 위한 **벨만 최적 방정식(Bellman Optimality Equation)**은 다음과 같습니다.

이는 가능한 모든 행동 중 가장 큰 기대 보상을 주는 행동을 선택한다는 의미입니다.
행동 가치 함수의 형태로 쓰면 다음과 같습니다.
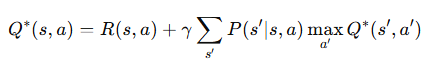
이 식은 Q-learning의 기본 구조로, 현재 행동의 가치가 “즉시 보상”과 “다음 상태에서 가능한 최선의 행동의 가치”의 합으로 계산된다는 것을 의미합니다.
벨만 방정식의 해법
벨만 방정식을 실제로 푸는 대표적인 방법은 가치 반복(Value Iteration)과 정책 반복(Policy Iteration)입니다.
가치 반복은 모든 상태의 가치를 임의의 값으로 시작한 뒤, 벨만 방정식을 반복적으로 적용하여 각 상태의 가치가 수렴할 때까지 갱신하는 방법입니다. 이 과정을 통해 최적의 가치함수 V*(s)를 구하고, 이후 각 상태에서 최대 값을 주는 행동을 선택하여 최적 정책 π*(s)를 도출합니다.
정책 반복은 먼저 임의의 정책을 설정하고, 그 정책을 따를 때의 가치를 계산하는 정책 평가 단계와, 계산된 가치를 바탕으로 더 나은 행동을 선택하는 정책 개선 단계를 번갈아 수행하는 방법입니다. 이 과정을 반복하면 정책이 더 이상 변하지 않는 최적 정책에 도달하게 됩니다.
예시로 이해하기
예를 들어, 상태 S에서 목표 상태 G로 이동할 때 보상이 +10이고 할인율 γ가 0.9라고 가정해 보겠습니다. 이때 G는 종료 상태이므로 V(G)=0이며, S에서 한 번 이동하면 바로 G에 도달합니다. 따라서

이 됩니다.
하지만 만약 S에서 G로 갈 확률이 80%이고, 제자리에 머물 확률이 20%라면 식은 다음과 같이 바뀝니다.

이 경우, 확률적 불확실성이 반영되어 실제 기대 가치는 이전보다 낮아지게 됩니다.
HMM과 MDP의 차이
HMM과 MDP는 모두 마르코프 모델에 기반을 두지만 목적이 다릅니다. HMM은 상태를 직접 관찰할 수 없고, 대신 관측 데이터를 통해 상태를 추정하는 모델입니다. 반면 MDP는 상태와 행동이 모두 명확히 관찰 가능한 상황에서 최적의 행동을 선택하는 문제를 다룹니다. 즉, HMM은 “상태를 추정”하는 모델이고, MDP는 “행동을 결정”하는 모델입니다.
할인율의 의미
할인율 γ는 단순히 수학적 계산을 위한 요소가 아니라, 시간의 가치를 반영하는 중요한 개념입니다. 현실적으로 사람이나 시스템은 “현재의 보상”을 “미래의 보상”보다 더 높게 평가하는 경향이 있습니다. 따라서 γ는 이러한 시간적 선호를 반영하고, 동시에 무한히 먼 미래의 보상 합이 발산하지 않도록 만들어 수학적 안정성을 보장합니다.
응용 분야
마르코프 모델과 벨만 방정식은 인공지능, 로봇공학, 경제학, 의학, 교통 등 다양한 분야에서 활용됩니다. 예를 들어 추천 시스템에서는 사용자의 현재 상태를 분석하여 가장 적절한 콘텐츠를 추천하고, 자율주행에서는 차량이 주변 환경을 인식하여 최적의 주행 경로를 선택합니다. 또한 재고관리에서는 수요 예측을 기반으로 발주 시점을 결정하고, 의료 의사결정에서는 치료 효과를 극대화하기 위한 정책을 설계할 때 사용됩니다.
마르코프 모델은 “현재 상태가 미래를 결정한다”는 단순하면서도 강력한 원리를 통해 복잡한 확률적 시스템을 단순화하여 설명할 수 있도록 해 줍니다. 벨만 방정식은 이러한 시스템 속에서 “현재의 가치”를 “즉시 보상”과 “미래의 기대 가치”로 분해하여 계산할 수 있게 해 주는 수학적 도구입니다. 두 개념은 강화학습의 이론적 기초를 이루며, 불확실한 환경 속에서도 최적의 의사결정을 내릴 수 있도록 돕는 핵심 원리로 활용되고 있습니다.
'인공지능 > 딥러닝 -파이썬 인공지능' 카테고리의 다른 글
| 하이퍼볼릭 탄젠트 함수 (0) | 2025.10.22 |
|---|---|
| RNN (0) | 2025.10.22 |
| CNN, MNIST 코드 분석 (0) | 2025.09.10 |
| 패션 MNIST 소스 분석 (1) | 2025.09.10 |
| RNN(순환 신경망), LSTM 그리고 cs231n (1) | 2023.11.12 |


